Tema 3. Descripción de las fuerzas en el entorno.

Tema 3. La descripción de las fuerzas en el entorno

La fuerza; resultado de las interacciones por contacto ( mecánicas) & a distancia (magnéticas & electrostáticas), & representación con vectores.

 La fuerza es

 un concepto difícil de definir, pero muy conocido. Sin que nos digan lo que es la fuerza podemos intuir su significado a través de la experiencia diaria.

Una fuerza es algo que cuando actúa sobre un cuerpo, de cierta masa, le provoca un efecto.

Por ejemplo, al levantar pesas, al golpear una pelota con la cabeza o con el pie, al empujar algún cuerpo sólido, al tirar una locomotora de los vagones, al realizar un esfuerzo muscular al empujar algo, etcétera siempre hay un efecto.

El efecto de la aplicación de una fuerza sobre un objeto puede ser:

Modificación del estado de movimiento en que se encuentra el objeto que la recibe Modificación de su aspecto físico.

Fuerza de interacción por contacto: Los cuerpos deben estar en contacto (tocándose) para ejercerlas y para recibir su efecto.  Por ejemplo: cuando nos apoyamos en una pared, empujamos un banco, escribimos, pateamos una pelota, nos colgamos de una soga, etc.

Son fuerzas de interacción por contacto: La fuerza normal, empuje, tensión, rozamiento, elástica, etc.

Fuerza de interacción a distancia:  Los cuerpos no necesariamente deben estar tocándose para ejercer y recibir su efecto. Por ejemplo: cuando cae un cuerpo, un imán atrae a un alfiler, etc.

Son fuerzas de interacción a distancia: la fuerza gravitatoria, eléctrica, magnética.

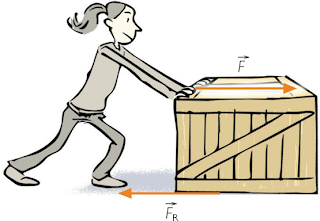
Representación de la Fuerza con vectores.

La fuerza es una cantidad vectorial; es decir tiene magnitud, dirección y    sentido. Por ser un vector Gráficamente, se representa por un segmento de recta con una punta de flecha en uno de sus extremos, donde el tamaño de esta es la magnitud, la punta de la flecha indica el sentido y el ángulo la dirección.

Vectorialmente se denota con la letra (F) con una flecha sobre la misma o con la letra sola en negrita. Su magnitud letra sola o el vector entre barras verticales.

Fuerza resultante

Si sobre un cuerpo actúan varias fuerzas se pueden sumar las mismas de forma vectorial (como suma de vectores) obteniendo una fuerza resultante, es decir equivalente a todas las demás. Si la resultante de fuerzas es igual a cero, el efecto es el mismo que si no hubiera fuerzas aplicadas: el cuerpo se mantiene en reposo o con movimiento rectilíneo uniforme, es decir que no modifica su velocidad.

En la mayoría de los casos no tenemos las coordenadas de los vectores sino que tenemos su módulo y el ángulo con el que la fuerza está aplicada. Para sumar las fuerzas en este caso es necesario descomponerlas proyectándolas sobre los ejes y luego volver a componerlas en una resultante (composición y descomposición de fuerzas).

Métodos gráficos de suma vectorial.

Para utilizar métodos gráficos en la suma o resta de vectores, es necesario representar las cantidades en una escala de mediciónmanipulable. Es decir, podemos representar un vector velocidad de 10 m/s hacia el norte con una flecha indicando hacia el eje y positivo que mida 10 cm, en la cual, cada cm representa una unidad de magnitud real para la cantidad (1 m/s).

El vector que resulta de operar dos o más vectores, es conocido como el vector resultante, o simplemente la resultante .

El método del paralelogramo permite sumar dos vectores de manera sencilla. Consiste en colocar los dos vectores, con su magnitud a escala, dirección y sentido originales, en el origen, de manera que los dos vectores inicien en el mismo punto. Los dos vectores forman dos lados adyacentes del paralelogramo. Los otros lados se construyen trazando lineas paralelas a los vectores opuestos de igual longitud. El vector suma resultante se representa a escala mediante un segmento de recta dado por la diagonal del paralelogramo, partiendo del origen en el que se unen los vectores hasta la intersección de las paralelas trazadas.

Ejemplo. Una bicicleta parte desde un taller de reparación y se desplaza (4 m,30º) y luego (3 m, 0º). Encuentre el desplazamiento total de la bicicleta, indicando la dirección tomada desde el taller.

El desplazamiento total se da en dos tramos. Cada tramo desplazado se representa por los vectores d1 y d2. El desplazamiento total es D = d1 y d2.

Los dos vectores son dibujados a la misma escala, y se colocan en el mismo origen. Luego se trazan las lineas paralelas.

Si medimos con una regla, a la escala dada, el tamaño del vector resultante debe dar aproximadamente 6.75 unidades de la escala; es decir, la magnitud del vector desplazamiento total es de 6.75 m.

La medida de la dirección se toma con la ayuda de un transportador, y debe dar aproximadamente 17º desde el origen propuesto. El sentido del vector resultante es positivo, según el marco de referencia común (plano cartesiano, hacia x positivo y hacia y positivo). Entonces como resultado, la bicicleta se desplaza (6.75 m,17º).